ВВЕДЕНИЕ В МАГИЮ ФУНКЦИЙ И ИНТЕГРАЛОВ

Здравствуйте, студенты Вуза Аргемоны! Рада видеть вас на своем уроке!

Зовут меня Чжоули. С сегодняшнего дня мы начнём изучать новый, достаточно интересный предмет — Магию функций и интегралов. Первый урок будет вводным, и постараемся вместе понять, а для чего всё это магу надо знать.

Сразу скажу важную мысль. Если вдруг вам данная лекция-введение в предмет покажется непонятной и вы не будет знать, как ответить на некоторые вопросы, попробуйте заглянуть на следующие лекции первого модуля. Они достаточно простые, посвящены элементарным функциям и основаны на материале маггловской школы 6-11 классов. Возможно, пройдя следующие лекции, вы поймёте, как отвечать во введении. А возможно это понимание придёт только в конце предмета. Ничего страшного. У всех начальная подготовка разная, и изучением данного предмета это можно изменить. Поэтому не опускайте сразу руки от непонимания.

А теперь продолжим нашу лекцию.
Ну то, что магия творится не просто так, по простому мановению волшебной палочки, вы уж точно знаете, в отличии от новичков нашего мира. И также знаете, что для сотворения волшебства надо очень постараться и вспомнить сведения из многих областей знаний.

Помните, как Вовка попал в Тридевятое царство и думал, что волшебству научиться раз плюнуть? Вот три волшебницы приехали на слёт юных волшебниц и показывали своё мастерство.

Одной рукой махнули — озеро появилось, второй — лебеди по нему поплыли. Дворец, как по заказу, на глазах вырос. Вовка очень обрадовался, что наконец-то он может что-то сделать, не прилагая к этому никаких усилий — ни физических, ни умственных. И каково же было его разочарование, когда волшебницы усадили Вовку за парту и приступили к обучению магии.

И, оказалось, чтобы построить дворец, надо сделать кучу расчётов: сколько блоков, из какого материала надо взять и как их сложить. А чтобы появилось озеро, так вообще надо решить проблему, откуда вода будет втекать и куда вытекать, чтобы озеро не залило всё вокруг.

А посмотрите, какие дома маги пытаются строить! Дипломница Хогвартса Сириуса Куница поездила по миру и собрала целую коллекцию таких домов.
Вот как этот дом держится на своей опоре?

Но можно этому и не удивляться, вспомнив практику некоторых магов строить удивительные сооружения из камней.

Нет здесь никакого фокуса с магосуперклеем, который прочно соединяет камни друг с другом. Нет никаких дополнительных приспособлений, заставляющих камни так удерживаться в равновесии. Тут задействованы только руки и ум, который позволяет высчитывать центр тяжести очередного камня и найти то место во всей структуре, куда и каким образом надо поставить камень, чтобы всё остальное сооружение не рухнуло. Конечно, налетевший сильный порыв ветра разрушит данную конктрукцию, но даже то, что она держится несколько минут, поражает воображение окружающих. А делающие их маги ради нескольких минут такой парящей каменной красоты проводят часы в поисках равновесия, а помогают им в этом функции и интегралы. Теперь понятно, как удерживается в равновесии тот дом.

А вот другой пример дома.

Какие изящные линии! Какая симметрия! И только функции могут дать такую красоту линий. Как известно, симметрия как раз и придаёт миру гармонию и совершенство. То, что математическими законами можно описать всё в мире, известно уже давно. Именно математика правит миром. И хоть красота — понятие туманное, но именно она служит источником вдохновения. Когда дальнейший путь не ясен, именно математическая красота ведет учёных (вот уж кто истинные маги) к истине. Физик интуитивно чувствует, что природа предпочитает красивые «решения» некрасивым. Эйнштейн Гейзенберг однажды заметил: «Если природа приводит нас к математическим выражениям необычайно простым и красивым... которые ранее не встречались, то мы невольно воспринимаем их как „истинные“ и считаем, что они открывают то или иное свойство природы».

Смотря на разные функции и изучая их свойства, поражаешься разумности природы и красоте её математического представления.

В чём могут помочь магам интегралы? Оказывается, с их помощью легко вычислить то, к чему даже и не знаешь, как изначально подступиться.

Ну самое простое и самое, на мой взгляд, захватывающее поначалу — это вычисление площади криволинейной трапеции.
Что такое трапеция, думаю, вы помните. Четырехугольник, у которого две противоположные стороны параллельны. Однако, все стороны этого четырехугольника — прямые, а у криволинейной трапеции одна из сторон, как вы догадались из названия, представляет собой произвольную кривую.

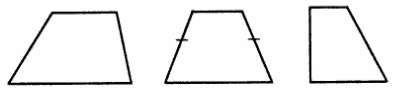
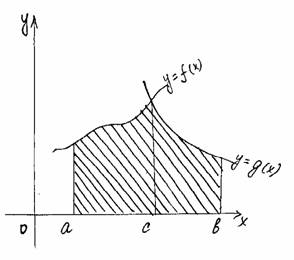
Слева пример трёх основных видов трапеции: произвольной, равносторонней и прямоугольной, а справа заштрихованная область — это и есть криволинейная трапеция. Верхняя её сторона — кривая, состоящая их двух функций.

Следующее, что можно легко вычислить с помощью интегралов, — это площадь любой поверхности. Известными способами можно вычислить площади только известных фигур — многоугольников, круга, эллипса. А если фигура с кривыми сторонами, то сделать это не так-то просто. А интеграл даёт очень красивое и простое решение.

Вычисление объёма тела — это следующая сфера практического приложения интеграла. Есть известные формулы для вычисления параллелепипедов, пимамид, конусов, цилиндров, сферы, но как только перед нами тело другой формы, то, кроме того, как бросить его в ванну и подобно Архимеду смотреть, сколько воды это тело вытеснило, другого способа и нет. А если тело большое? И в ванну его никак не поместить? Вот, например, тело, полученное вращением произвольной кривой y=f(x) вокруг оси ОХ.

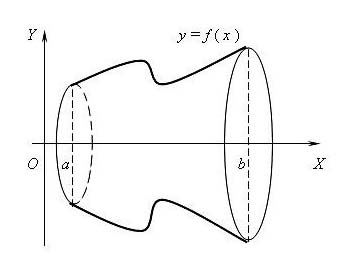
Вычислить объём такого тела непросто, а интеграл с этим справляется на раз.

Вычисление длины кривой. Тоже не всегда можно растянуть кривую и линейкой измерить её длину, а если знать, по какому закону эта кривая формируется, то можно легко вычислить её длину, не «снимая с места».

Вычисление центра тяжести тела. Для чего это надо, я рассказывала выше.

Это основные сферы приложения интегралов. По мере изучения я буду обращать ваше внимание и на другие задачи, которые легко решаются с помощью интегралов. Но понятие "интеграл" неразрывно связано с понятием «функция», поэтому с них мы и начнём наш курс. Сейчас я расскажу о понятии «функция», и на этом наш вводный урок закончим. «Функция» — очень важное (даже можно сказать, наиважнейшее) понятие в математике. Поэтому надо в этом разобраться очень аккуратно. Тогда будет намного легче усваивать следующие знания.
Итак, функция — это зависимость одной переменной (она называется «множество значений функции») от другой (а это «область определения функции»), при которой каждому значению из области определения ставится в соответствии одно и только одно значение из области значений.
Чаще всего в качестве переменной области значений выступает переменная y, а в качестве области определения служит х, но могут быть и другие. Сама зависимость в общем виде обозначается через f, g, h и т.д.
Например, y=f(x), u=g(v). Но мы чаще будем изучать конкретные функциональные зависимости.

Виды кривых, получаемых при распознавании функциональной зависимости на графике, который является наглядным изображением функции, может быть самым разным (мы будем ещё учиться по зависимости раскрывать явное лицо функции), но непременное свойство функции — каждому значению из области определения ставится в соответствии одно и только одно значение из области значений — сохраняется всегда.

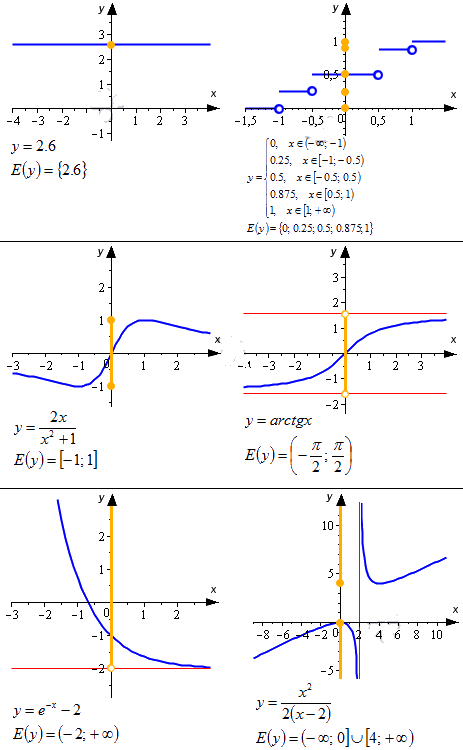
Вот примеры самых разных функций. Жёлтым обозначена область значений. Где-то это одно число, где-то набор конкретных чисел, а где-то целые численные интервалы.

Думаю, на сегодня информации вам достаточно, поэтому перейдём к домашнему заданию.

Задание 1. Поразмышляйте на основе информации, данной в лекции, где магу может помочь знание интегралов, приведя более-менее конкретные примеры самых разных ситуаций.

Задание 2. А сейчас прочитайте отрывок из книги Ольги Громыко «Профессия — ведьма»:

Сняв с шеи шнурок с авантюрином, я острым концом зуба стала выцарапывать на полу линии и руны. Одновременный перенос трёх человек требовал концентрации куда большей, чем можно было добиться просто в уме. Помощь Лёна не понадобилась. Формулы всплывали в памяти по мере надобности.
— Ты уверена, что эта гхырь сработает? — тролль первым не выдержал томительного ожидания.
— На пятьдесят процентов!
— Выходит, столько же приходится на второй вариант?
— Эти пятьдесят какие-то более вероятные.
— Так действуй, а не трепись!
— Хорошо, хорошо... Не торопи меня!
Я провела последнюю линию, искренне надеясь, что треугольник вышел равносторонним. Свеч у меня не было, их заменили лучины, нащепанные из факела. Хрупкий, неровный огонь едва держался на обугленных кончиках, малейшее движение воздуха могло свести на нет все мои старания. Сам факел пришлось потушить, чтобы он не оттягивал на себя чары. Лучины чуть тлели, самый осторожный взмах руки повергал их в трепет. То, чем я занималась, не лезло ни в какие рамки — начиная с того, что из-за слабой освещённости я почти не видела земли и могла промахнуться при вычерчивании, неточно соединив линии. Самые маститые маги пользуются отполированной до блеска доской, загодя расчерченной, с гнездами для свеч. Моя вдохновенная импровизация напоминала шаманский обряд в глухой деревеньке. Не хватало только восторженных воплей экзальтированной толпы да визга чёрного поросёнка на жертвеннике.
— Вольха, не отвлекайся.
Растворённый в темноте, Лён был моей незримой опорой. Пока он стоял рядом, — я слышала его ровное дыхание, чувствовала лёгкое касание его руки, вдыхала знакомый запах сильного, уверенного в себе и во мне мужчины, — я была неуязвима и всесильна.
— Встаньте напротив углов треугольника, но не касайтесь их, — резко скомандовала я. Итак, глубокий вдох...
Заклинаю вас, стихии небесные, дыханьем своим,
Заклинаю вас, стихии огненные, пламенем, горящим в сердце моём,
Заклинаю вас, стихии водные, кровью своей,
Заклинаю вас, стихии земные, смертной плотью человеческой,
Возьмите частицу себя, узнайте дочь свою,
Подчинитесь моей воле!
Я коротко и зло полоснула себя поперёк ладони осколком гранита. Проклятые лучины опасно замигали, нарушая концентрацию. Прикусив губу, я отбросила камень и сложила ладони "лодочкой", наполняя их кровью. Знакомая боль стянула низ живота стальным обручем, переходя в жаркую пульсацию силы.
Я не единожды наблюдала обряды на крови, даже участвовала в них — под наблюдением Учителя. «Кровь — это жизнь, — нараспев говорил он, как бы походя вычерчивая магические знаки воздетыми руками. — Жизнь — это сила. У жизни есть начало и конец. Как и у силы. Она прирастает по дуге и по дуге же убывает. Для максимальной отдачи вы должны почерпнуть её в момент наивысшего расцвета. Сосредоточьте своё заклинание в точке между концами дуги, не торопитесь, но и не мешкайте. Ваша задача — не с выражением пробормотать заклинание, но распознать в тысячелетии ожидания мгновение действия».
Итак, точка максимума. Дождаться точки. Сплести заклинание. Всё очень просто.
В прошлый раз мне это не удалось. Опоздала на долю секунды, и дуга круто нырнула вниз, бесцельно распылив силу — под ехидное хихиканье одноклассников.
Сила прирастала. Кончики пальцев засветились, время замедлилось, звуки растянулись в невнятный монотонный гул, всё тело превратилось в вибрирующий конденсатор. Может, уже пора? Нет, ещё на подъёме. Подождать... подождать ещё чуть-чуть, отогнать прочь голодную пасть нетерпения, рвущую сердце ледяными клыками... Только не спеши... Только не опоздай... Нет уже ни звуков, ни света лучин, ни серых стен пещеры — только ослепительно белый поток света, растворяющий сознание... Бесконечная дуга уходит вверх... Бесконечная ЛИНИЯ.
И тут мне стало по-настоящему страшно. СИЛА НЕ КОНЧАЛАСЬ, нарастая подобно лавине, вызванной падением одного-единственного камушка. Всё новые и новые её пласты поднимались из горсти с кровью, завихряясь вокруг меня светящимся полупрозрачным коконом.
Отступать было поздно. Леший с ним, с максимумом! Я развела ладони, кровь горящим комом полетела в центр треугольника и, не расплескавшись, беззвучно вошла в пол. Треугольник мгновенно раскалился добела, над ним нарисовалась безглазая череповидная морда, с рявканьем щёлкнула пастью, принимая мою жертву, и совсем не прочь принять кое-что посущественнее. Освобождённая сила хлынула в матрицу заклинания, гневно забурлила в слишком тесной оболочке, норовя разнести её в клочья. Я инстинктивно вскинула руки в защитном жесте, корявые линии мигнули, лучины вспыхнули по всей длине и рассыпались в пепел.

Попробуте поразмышлять:
— Почему Вольха нарисовала равносторонний треугольник?
— Какие формулы она могла вспоминать?
— Какие ещё расчёты она делала?

Задание 3. Возьмите копии последнего свитка с функциями и докажите с помощью карандаша или пера для каждого графика, что это именно функция.

Задание 4. А вот вам ещё один свиток, где в осях координат изображена окружность.

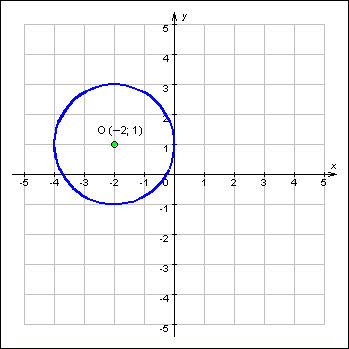
А что, и зависимость для неё есть. Вот такая: (x-x₀)² + (y-y₀)² = r². Для нашей окружности r=2, x₀=-2, y₀=1. Зависимость-то есть, а вот это не функция. Требуется доказать, что окружность — это не функция. Можете использовать этот пергамент, но потом мне его покажите вместе с доказательством.
Получилось? Теперь поделите эту окружность на две части линией, проходящей через центр окружности и параллельной оси ОХ. Рассмотрите отдельно две получившиеся полуокружности и установите: эти кривые — функции или нет?
Потом разделите данную окружность линией, проходящей через центр окружности, но параллельной оси ОУ. Вы так же получите две отдельные линии — две полуокружности. Функции это или нет? Тоже это докажите графически.

Давайте определимся, в каком виде сдавать домашнее задание. Из-за сложностей рисования на компьютере графиков вы можете делать их на пергаменте пером или карандашом, а потом прилагать к работе скрин (или фото) вашего пергамента, с пояснениями. Если придумаете какой другой способ, удобный лично для вас, то тоже можете использовать. Но главное, чтобы и мне было удобно читать и оценивать вашу работу.

Удачи!

Отправляйте работы через ЛИЧНЫЙ КАБИНЕТ
Свои вопросы смело можете передать с Персефоной