ВОЛНЫ, КОЧКИ, ПОРТАЛЫ И МАГИЯ ИСЧЕЗНОВЕНИЯ

Здравствуйте, уважаемые студенты вуза Аргемоны! Заглянули на лекцию, привлечённые её названием?)) Знаете, мне тоже интересно оказалось то, к чему я пришла в своих логических рассуждениях, готовясь к этой лекции. Ведь я фактически тоже открываю для себя магию функций во время подготовки к очередной встрече с вами. Поэтому хочется сразу поделиться найденным и выслушать ваши мнения на этот счёт. А может у кого ещё какие мысли интересные возникнут в процессе чтения лекции или подготовки домашнего задания?

Ну, это было лирическое отступление, а сейчас приступим к новой лекции.
Сегодня последняя лекция первого модуля, в рамках которого мы вспоминаем элементарные функции (а некоторые, может, заново знакомятся с ними, потому как основательно их забыли) и применяем к ним магию преобразования разного вида.
Нам осталось рассмотреть тригонометрические функции. Их четыре:

y = sin(x)
y = cos(x)
y = tg(x)
y = ctg(x)

Думаю, вы помните, как они называются, но всё же напомню для тех, кто, может быть, подзабыл: это синус, косинус, тангенс и котангенс. Причём две последние выражаются через первые две:



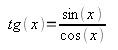
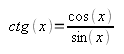
Я рассмотрю на уроке подробно функции синуса и котангенса, а вам останется в домашнем задании по аналогии провести исследование двух оставшихся функций.

Итак, функция синуса. График его следующий


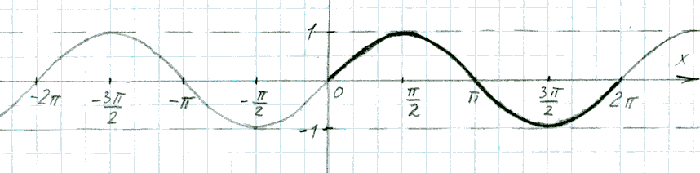
По графику сразу видно отличительную особенность этой функции от всех ранее изученных: какая-то часть графика повторяется то и дело. На рисунке эта часть выделена более чётко - это кусок от 0 до 2π. Длина этой части графика, как легко вычислить, как раз 2π, и называется она периодом данной функции, а сама функция синуса - периодической. π - это то самое число, которое равно 3,14... (в радианах) или 180° (в градусах). Я не буду останавливаться на этом подробно, потому как можно в объяснении уйти очень далеко и глубоко. Наша цель - функция и её график, а всё остальное (если не помните) вам придётся либо принять на веру как аксиому, либо прибегнуть к помощи зверика гугл и почитать, что он вам скажет на этот счёт.

Думаю, надо вкратце напомнить, что такое есть синус и косинус. Начертим единичную окружность - окружность, радиус которой равен 1. И пустим вращаться по этой окружности точку.



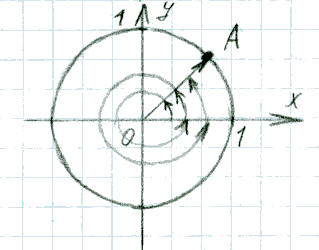
Эта точка в любой момент времени имеет какие-то определённые координаты. Так вот, абсцисса точки (координата её по оси ОХ) и есть косинус угла, который образует радиус-вектор точки с осью ОХ. Радиус-вектор - это линия, соединяющая начало координат с данной точкой. А ордината точки - это синус этого же угла.
Видно, что после того, как точка совершит полный оборот по окружности, она пойдёт опять по той же самой линии, т.е. координаты точки будут те же, а вот углы другие. Полный оборот по окружности - это 360° или 2π (в радианах). Например, угол точки А может быть равен и 45°, и 405° (360+45 - один полный оборот), и 765° (360+360+45 - два полных оборота), и т.д.
Это как раз и подтверждает, что период синуса (равно как и косинуса) равен 2π.
Когда точка вращается против часовой стрелки - углы получаются положительные, а если точка вращается по часовой стрелке - то отрицательные.

Из графика синуса видно, что областью определения является вся числовая прямая (все действительные числа), т.е. функция синуса не имеет особенностей и определена на всей оси ОХ.
А что происходит с множеством значений этой функции? Ещё раз поглядите на единичную окружность, из которой видно, что значение ординаты (синуса) меняется только в пределах от -1 до +1 и не может принимать других значений, например, +2, или -3, и другие. Это же касается и множества значений, которые может принимать косинус. На графике синуса это тоже хорошо видно: весь график помещается как будто в трубе, между двумя прямыми: у=-1 и у=1.
График представляет собой волну, поэтому участки возрастания функции чередуются с участками убывания. Не буду указывать точные границы этих участков, это сейчас не так важно. Важен общий вид функции.

А теперь попробуем применить к этой функции уже известные вам виды магии преобразования.

Сначала добавим какое-то число к х:
y = sin(x+a)
Помните, что происходит с графиками при таком преобразовании? Да-да, эта магия вызывает горизонтальный перенос графика вдоль оси ОХ. Причём, если а>0, то график сдвигается влево. Если a<0, то вправо. Область определения и множество значений при такой магии не меняются.



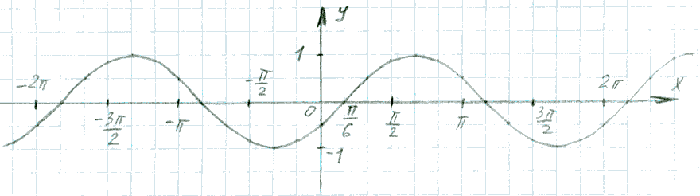
На рисунке я сдвинула график вправо на π/6, значит, функция имеет вид:
y = sin(x-π/6)
Но что интересно: если сдвинуть функцию на π/2 влево, то мы получим график косинуса, т.е.
sin(x+π/2) = cos(x)

А теперь применим магию вертикального сдвига. Добавим какое-то число в качестве слагаемого к самому синусу:
y = sin(x+a) + b

График сдвинется на b единиц вверх, если b>0, или вниз, если b<0. Как видно, соответственно изменится множество значений, а область определения остаётся прежней.
Перенесу тот график, который я сдвигала на π/6 вправо, на 0.5 единиц вниз:
y = sin(x-π/6)-0,5



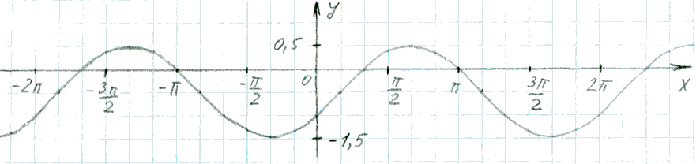
Если изначально множество значений представляло собой промежуток [-1; 1], то после вертикально сдвига он стал равным [-1+b; 1+b]. В нашем случае [-1,5; 0,5].
Впрочем, ширина "коридора" не изменилась и по-прежнему составляет 2 единицы.

Неужели синусу предназначено всё время томиться в "узком коридоре" шириной 2 единицы? Оказывается, есть ещё один вид магии, который позволяет расширить этот "коридор". Совсем его убрать не получается, но сделать шире - вполне можно. Достаточно добавить число перед самим синусом в качестве множителя.

y = k*sin(x)



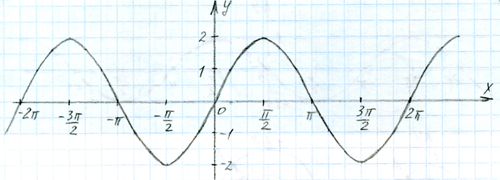
Чем больше число k, тем шире получается "коридор", внутри которого колеблется наша синусовая волна. Однако, можно и значительно уменьшить этот "коридор" с помощью маленького по величине множителя перед синусом.
В нашем случае k=2.

Какую магию мы ещё можем испробовать? Магию минуса. Этот вид магии те части графика, которые находятся выше оси ОХ, опускает вниз, а нижние - поднимает наверх. Другими словами, график функции отражается относительно оси ОХ.



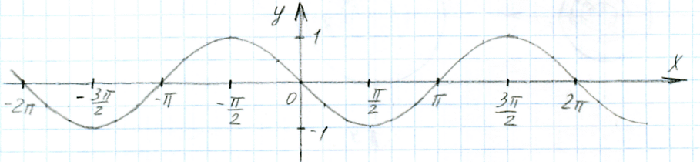
Кстати, функция синуса - нечётная, т.е sin(-x) = - sin(x). А вот функция косинуса - чётная: cos(-x) = cos(x). Это замечание вам поможет при выполнении домашней работы.

Новый вид магии - магия сжатия или растяжения. Чтобы активировать этот вид магии, надо просто поставить коэффициент перед х в качестве множителя

y = sin (c*x)

Если |c|>1, то волны сожмутся, а если |c|<1, то будем наблюдать растяжение. Соответственно, меняется период функции. При |c|>1 период уменьшается в |c| раз, а если |c|<1, то уменьшается в |c| раз, но фактически увеличивается в 1/|c| раз.



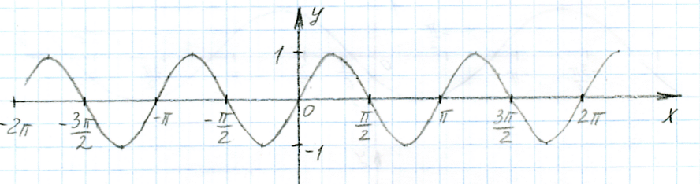
Здесь c=2. Период равен π (2π/2).



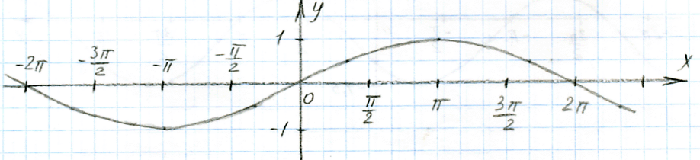
А здесь с=1/2. Период равен 4π (2π/(1/2)=2π*2=4π).

Перед тем, как перейти к последнему виду магии, который мы применим к функции синуса, хочу подвести промежуточный итог и рассказать, в каком порядке действуют различные виды магии, когда они встречаются все вместе в одном месте... вернее, в одной функции.

y = k*sin(c*x+a) + b

Итак, мы хотим применить к данной элементарной функции y=sin(x) четыре вида магии. Просто так, без порядка, их применять нельзя. Порядок тут очень необходим, иначе можно получить совсем не тот результат, на который рассчитывал.
Но чтобы начать применять магию, надо сделать небольшое преобразование под знаком синуса.

y = k*sin(c*(x+a/c)) + b

Первой надо применить магию коэффициента a/с. То есть сначала надо синусовую волну сдвинуть по оси ОХ, соответственно, влево или вправо, если этот коэффициент положительный или отрицательный.
Потом применяем магию коэффициента c, то есть сжимаем или растягиваем волну.
Затем приступает к своей работе магия увеличения или уменьшения - это действие коэффициента k.
И, наконец, уступается место для развёртывания магии коэффициента b - магии вертикального переноса функции.

И последний вид магии, который мы применим, - это магия модуля.

y = |sin(x)|

Мне, например, очень нравится этот вид магии, который иногда даёт поразительно красивые результаты. Вот и сейчас он превратит нашу плавную волну в "дорожку кочек" (все те части графика, которые находятся ниже оси ОХ, отражаются относительно неё), по которым можно очень легко прыгать.



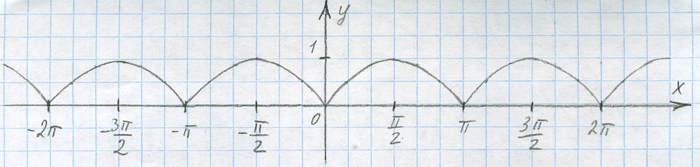
Хотела было перейти к следующей функции, но тут промелькнула мысль показать вам вот эту, вроде бы очень простую на первый взгляд, функцию:

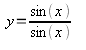
Казалось бы, чего проще: числитель равен знаменателю, поделим их друг на друга и получим простую функцию у=1. Это прямая, параллельная оси ОХ и проходящая через точку (0; 1).
Однако, не всё так просто. Не зря же синус стоит в знаменателе, и просто так разделить на него нельзя. Ведь есть такие значения х, в которых синус обращается в ноль, а на ноль, как известно, делить нельзя. Поищем эти особые точки.

sin(x)=0
x=πn, где n∈Z (множество целых чисел: 0, ±1, ±2, ...)
x=0; ±π; ±2π; ...

Их, особых точек, оказывается, очень много, и они располагаются на прямой у=1 в виде выколотых точек на расстоянии π друг от друга.



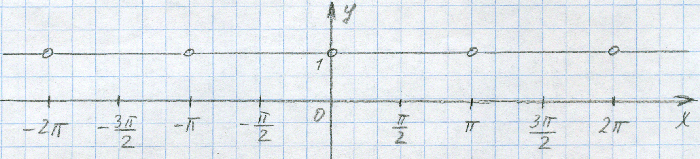
Посмотрите внимательно теперь на график: прямая с кучей выколотых точек. Что это? Вот идём по тропинке и вдруг - ничего, как будто провал в другое измерение. Наша реальность в виде выколотой точки нам подсказывает, что в этой точке реальности нет. Так может в ней существует нереальность или проход в параллельный мир? Нам ли, магам, бояться этой нереальности? Нам, наоборот, интересно всё такое нереальное изучить, пощупать и испробовать на себе.

А теперь перейдём к рассмотрению функции котангенса. На что сразу надо обратить внимание, так это на то, что эта зависимость представляет собой дробь. А если есть дробь - значит есть то, на что делится. В нашем случае делится на sin(x). Значит, функция котангенса не существует в тех точках x, где sin(x)=0. Эти точки мы уже вычислили выше. Попробуем выяснить, что же происходит с функцией котангенса при приближении к этим точкам?
Возьмём самую простую - точку 0. Обратимся к единичной окружности.



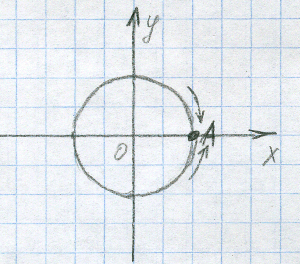
В этой точке косинус равен 1, а синус равен нулю. Но нас сейчас интересуют те точки, которые находятся в небольшой окрестности нуля. Видно, что в них значение синуса очень маленькое (положительное или отрицательное), а значение косинуса стабильное - около 1 (чуть меньше его). Если мы будем делить число, очень близкое к единице, на очень маленькое число, то получим очень большое число. Причём, чем на меньшее число мы делим, тем бОльшее число получаем. Значит, по мере приближения точки на единичной окружности к положению А, отношение косинуса к синусу будет либо стремиться в плюс бесконечность, когда точка приближается сверху (т.е. находясь в положительной области), либо в минус бесконечность, если точка приближается снизу (т.е. находясь в отрицательной области). И так ведёт себя котангенс во всех особых точках, которые мы нашли выше: слева от этой точки значение котангенса стремится в минус бесконечность, справа - в плюс бесконечность.
Так как никакого значения конкретно в этих точках котангенс не принимает, то надо признать, что тут мы имеем большое количество ассимптот - линий, к которым график функции стремится, но никогда не пересекает.
Так как график функции стремится и в плюс бесконечность, и в минус беконечность, то, конечно, есть точки, в которых график пересекает ось ОХ, т.е. где котангенс равен нулю, - это те точки оси ОХ, в которых косинус равен нулю

cos(x) = 0
x = π/2 + πn, где n∈Z (множество целых чисел: 0, ±1, ±2, ...)
x = ±π/2; ±3π/2; ±5π/2; ...

Котангенс - периодическая функция, с периодом, равным π.
Проведя такое исследование, нарисуем сам график котангенcа



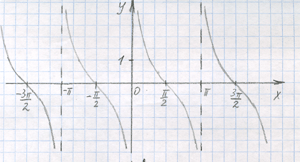
Видно, что он всё время убывающий.
Применим к этой функции магию горизонтального сдвига и вертикального переноса. Я не буду уже подробно это объяснять, только изображу на графиках. Думаю, все уже хорошо освоились с этими видами магии.

y = ctg(x+a) + b

     

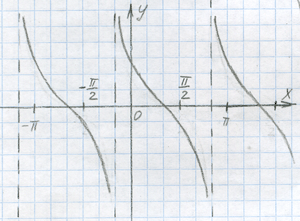
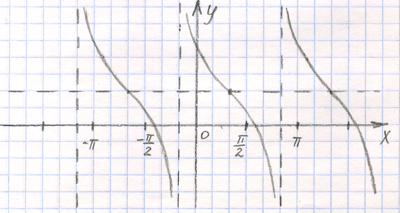
Что ещё можно применить к этой функции, чтобы увидеть красивый результат?

Далее у нас ещё остались магия минуса и модуля.
Минус (или это фактически множитель -1 перед функцией) вызывает отображение графика относительно оси ОХ.


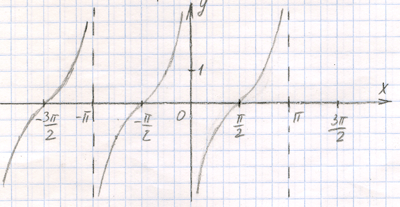
Ничего вам этот график не напоминает? Да, это тангенс, только сдвинутый по горизонтали на π/2. Причём неважно, в какую сторону.
Значит, получили
-ctg(x) = tg(x±π/2)

И теперь применим магию модуля
y = |ctg(x)|
Все части котангенса, расположенные ниже оси ОХ, отражаются относительно этой оси и получаем следующее



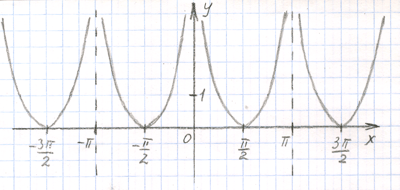
Похож график на параболу, правда? Но только внешне похож, а по поведению сильно отличается: веточки модуля котангенса приближаются к вертикальным линиям-ассимптотам, но никогда их не пересекают, а на ветви настоящей параболы такого ограничения нет.

Хотела вам дать ещё нахождение обратных функций, но решила, что хватит и того, что мы уже рассмотрели. Поэтому перейдём к домашнему заданию.

Домашнее задание.
Вам надо провести исследование функций y=cos(x) и y=tg(x), используя все те виды магии, которые были рассмотрены на уроке. В качестве коэффициентов a, b, c, k возьмите удобные для себя конкретные числа, но такие, чтобы наиболее разносторонне можно было увидеть все виды магии преобразования (советую k взять отрицательным числом, тогда можно совместить два вида магии). Не забывайте указывать область определения и множество значений.


Удачи!

Отправляйте работы через ЛИЧНЫЙ КАБИНЕТ
Свои вопросы смело можете передать с Персефоной