ТАКАЯ ПРОСТАЯ И ТАКАЯ СЛОЖНАЯ ПРЯМАЯ

Здравствуйте, студенты вуза Аргемоны! Я очень рада, что вы добрались до второй лекции.

Сегодня мы с вами поговорим о прямой. Казалось бы, что может быть проще прямой. Прямая — она и в Африке прямая. Это начальное понятие геометрии, не поддающееся никакому доказательству. Это понятие изначальное, такое же, как и точка. Но почему-то в головах некоторых образуется путаница, когда начинается работа с прямой. Поэтому сейчас постараемся собрать и систематизировать все сведения о прямой, которые вы получили в маггловской школе. Ведь прямые — это важная составляющая нашей жизни.

Задание 1. Где можно в окружающем мире наглядно увидеть прямую? Насколько, на ваш взгляд, велика роль прямой в жизни мира вообще?

Первое, что надо чётко запомнить, — в уравнении прямой переменные х и у обязательно присутствуют в первой степени.
Общий вид уравнения прямой следующий:

Ax + By + С = 0,            (1)

где A, B, C — произвольные коэффициенты, причём А и В не могут одновременно равняться нулю. Отсюда следует, что в уравнении могут быть как и х, и у, так и только х без у, и только у без х. Тогда получаются прямые, обладающие конкретными свойствами.

Задание 2. Опишите (и нарисуйте), что это за такие особенные прямые, когда в уравнении присутствует либо только х, либо только у, то есть уравнение прямой в таком случае имеет вид: y=a или x=b, где а и b — произвольные величины.

Для домашнего задания каждый возьмёт для исследования прямую, коэффициенты которой будут определяться следующим образом:
А — первая цифра номера вашего ЛД
В — вторая цифра номера вашего ЛД
С — третья цифра номера вашего ЛД (или A-B, если номер вашего ЛД — двузначный)

Как узнать номер своего ЛД? Я тут упустила тот момент, что в Аргемоне в свой личный кабинет учащиеся входят по имени, а не по номеру ЛД, как это было в ХС. Откройте список учащихся своего дома и нажмите на свой ник. Вы увидите страничку со своей личной информацией (впрочем, вы её видели). Обратите внимание на ссылку этой странички в строке браузера. Она имеет вот такой вид, например: http://argemona.ru/form/student/1384.html
Это ЛД Этельберты из Краннога. Номер её ЛД 1384. Теперь, я думаю, каждый найдёт свой.
А, вообще, архитектор Аргемоны сделала так, что сейчас каждый может видеть в своей личной информации номер своего личного дела.

Например, номер моего ЛД равен 11. Значит, А=1, В=1, С=1-1=0.
Уравнение моей прямой примет вид: х+у=0.

Для многих привычней уравнение прямой вот в таком виде:

у = kx + b            (2)

Однако очень легко преобразовать общий вид уравнения в последний вид.

Ax+By+C=0
By=-Ax-C
y=-(A/B)x-(C/B)

Обозначим: k=-(A/B); b=-(C/B) и получим привычное
y=kx+b

Запишу свою прямую в этом виде: у=-х
Для моей прямой k=-1; b=0.

В уравнении прямой (2) коэффициент k называется угловым коэффициентом прямой и равен тангенсу угла наклона прямой к оси ОХ. Поэтому уравнение (2) называется уравнением прямой с угловым коэффициентом.
Т.е. в моем случае, tgφ=-1. Угол φ=135º. Кстати, по знаку углового коэффициента можно сразу сказать, какой угол — острый или тупой — образует прямая с осью ОХ. Если коэффициент положительный, то угол острый, если отрицательный, то тупой. По сути, моя прямая — это биссектриса 2 и 4 координатных углов, и проходит моя прямая через точку пересечения координатных осей.



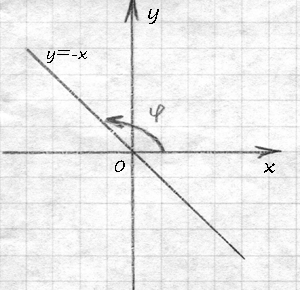
В виде (2) нельзя представить прямую, параллельную оси OY. Почему? Это будет 3-м заданием.

Задание 3. Почему в виде (2) нельзя представить прямую, параллельную оси OY? И какой она имееет вид?

Третье задание пересекается с заданием 2. Если вы на него ответили, то ответить на третье задание не составит труда.

И вообще, прямая вида y=kx проходит через начало координат. С помощью коэфициента k мы можем регулировать наклон нашей прямой в любую сторону. Это первая магия прямой, которой мы можем легко владеть.

Появление в уравнении коэффициента b означает параллельный перенос прямой на b единиц вдоль оси OY (если b>0, то прямая перемещается вверх, а если b<0, то прямая переносится вниз). Это уже второй вид магии прямой, которая достаточно легко поддаётся овладению.



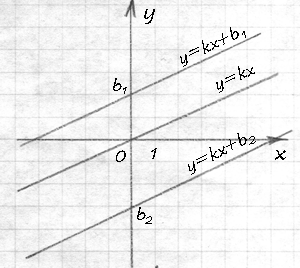
На рисунке b₁=2; b₂=-3.

Мы видим, что прямая отсекает на осях отрезки определённой длины, и, основываясь на этих фактах, можем записать уравнение прямой в отрезках:



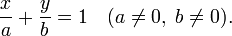
a и b — это отрезки, отсекаемые прямой на осях ОХ и ОY соответственно.
Ну, эта информация больше для интереса. В основном, мы будем пользоваться для прямой записями (1) и (2).

Напоследок, отмечу ещё один интересный факт. Всё же коэффициенты в уравнении прямой говорят о гораздо большем, чем мы можно предположить. Вернёмся к уравнению (1). Вектор с координатами {А, В} называется нормальным вектором прямой и перпендикулярен ей. А вектор {-В, А} или {В, -А} называется направляющим вектором прямой и параллелен ей. То есть, зная эти коэффициенты в уравнении прямой, можно определить, как направлена прямая.

Например, моя прямая x+y=0 имеет нормальный вектор {1; 1} и направляющий {1: -1} или {-1; 1}. Вектор можно переносить параллельно самому себе, и это будет считаться один и тот же вектор. То есть, рисуем его сначала по координатам (начало — в точке (0; 0), а конец — в высчитанных по коэффициентам точках) и потом переносим туда, куда нам удобнее. Ну, в моем случае я никуда векторы переносить не буду. И так видно, что нормальный вектор {1; 1} перпендикулярен моей прямой, а направляющие векторы {-1; 1} или {1; -1} располагаются прямо по прямой, но направлены в противоположные стороны.



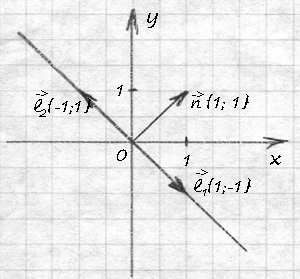
Видно, что прямая — это линия без каких-либо особенностей. Её областью определения являются все числа оси ОХ: (-∞; +∞), а множеством значений — все числа оси OY: (-∞; +∞).
Прямая либо возрастает на всей области определения, либо убывает. Моя прямая убывающая на всей области определения.

Однако, рассмотрим теперь вот такой пример:
     

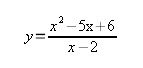
(3)


Вроде кажется, что непонятная совсем функция. Однако, давайте преобразуем выражение в числителе (надеюсь, вы помните, как разложить квадратный трёхчлен на множители — путём нахождения дискриминанта): x²-5x+6=(x-2)(x-3)

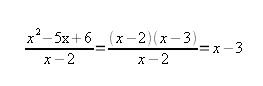
И в результате всех преобразований получаем функцию: y=x-3. Узнаётся сразу прямая. Она получается переносом вниз на 3 единицы прямой y=x (биссектрисы 1 и 3 координатных углов).
Только надо вспомнить, что мы изначальное выражение поделили на (x-2), и вообще первоначальная функция имела особенность (особенность — это те значения х, в которых не определена функция в своём первоначальном виде). На ноль делить нельзя, поэтому х-2 ≠ 0, т.е. х ≠ 2. И наша функция (3) определена на всей числовой прямой, кроме точки 2. Графический вид поэтому её такой: прямая с выколотой точкой



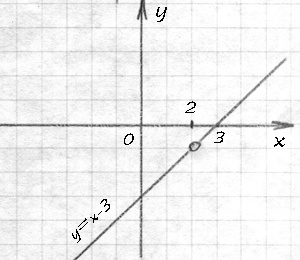
А теперь оставшееся домашнее задание:

Проведите исследование своей прямой:
— запишите уравнения прямой в общем виде (определите нормальный вектор прямой и направляющий);
— уравнение прямой с угловым коэффициентом (определите по тангенсу угла наклона, какой угол образует ваша прямая с направлением оси OX);
— нарисуйте график прямой и объясните, как эта прямая могла получиться из соответствующей прямой, проходящей через начало координат; укажите на графике все вектора;
— напишите уравнение вашей прямой в отрезках;
— убывает ваша прямая или возрастает.

А теперь исследуйте следующую функцию:


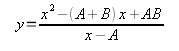
Значения A и В для каждого свои и определены в начале лекции. Подумайте, где маг может использовать прямую с выколотой (выколотыми) точкой.

Хотела вас уже отпустить домой, но вспомнила одну важную магическую функцию, связанную с прямой. Надо её тоже изучить. Это функция модуля

y=|x|

Уж очень часто на модулях ученики тоже спотыкаются, хотя ничего сложного тут нет. Определение модуля следующее:



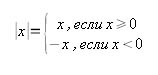
И график эта функция имеет следующий:



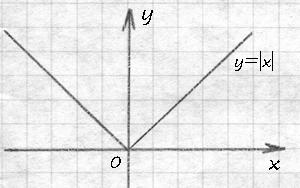
Видно, что эта функция на одной части области определения убывает, а на второй — возрастает.
Если у вас функция такая y=|kx+b|, то, соответственно, в зависимости от k, у графика оба «крыла» отклонятся от положения биссектрис, а «остриё» графика сместится в точку x=-b/k.



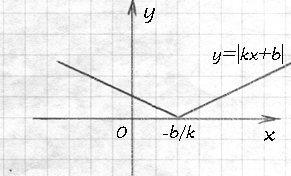
Как видим, с помощью модуля мы смогли переломить прямую. Это ещё один вид магии.
И последнее задание на дом:

Нарисовать функцию y=|kx+b|. У каждого k и b — свои. Расскажите, где маг может на практике использовать магию модуля (преломления прямой). И испробуйте сами магию минуса, то есть нарисуйте график функции y=-|kx+b| и исследуйте его.

И совсем самое последнее задание. Давайте подведём итог занятию. Перечислите все виды магии прямой, которыми вам удалось овладеть на этом уроке.

Вот теперь всё. Мы смогли пока рассмотреть простейшие (но в то же время основные) виды магии, с помощью которых мы можем управлять прямой. Не будем пока затрагивать прямую в пространстве. Если впоследствии она нам понадобится, то посвятим ей ещё урок. Что непонятно, уточняйте в КЦ. Всегда отвечу на любые вопросы. Главное, чтобы не оставалось ничего непонятным.

Удачи!

Отправляйте работы через ЛИЧНЫЙ КАБИНЕТ
Свои вопросы смело можете передать с Персефоной